Trinagon puzzles can be set up on any shape, that consists of more-or-less equilateral triangles.
The Polyhedra puzzles were the goal of the idea of trinagon. The hexagon only served as a leraning platform, and did surprise nevertheless.
With the polyhedra playgrounds, many intricacies of the game become visible. They are facets of difficulties that woul also be seen in a 'simple' rubiks cube.
Trinagon played on 3D shapes will often mix different symetries, or at least have odd symetries.
This already remarkably changes the puzzles mathematical design !
Trinagon played on 3D shapes will often mix different symetries, or at least have odd symetries.
This already remarkably changes the puzzles mathematical design !
Naturally the regular and convex shapes are the first that come to mind and the first that will be explored.
New 3D shapes are released as the game grows ! at present there are 22 playgrounds :
- 2 flat 2-dimensional hexagons
- and 2 folded planes.
these 2 can also be seen as parts of bigger shapes. One of them is strictly convex, the other is not. - all others are convex polyhedra.
A few examples of the playgrounds :
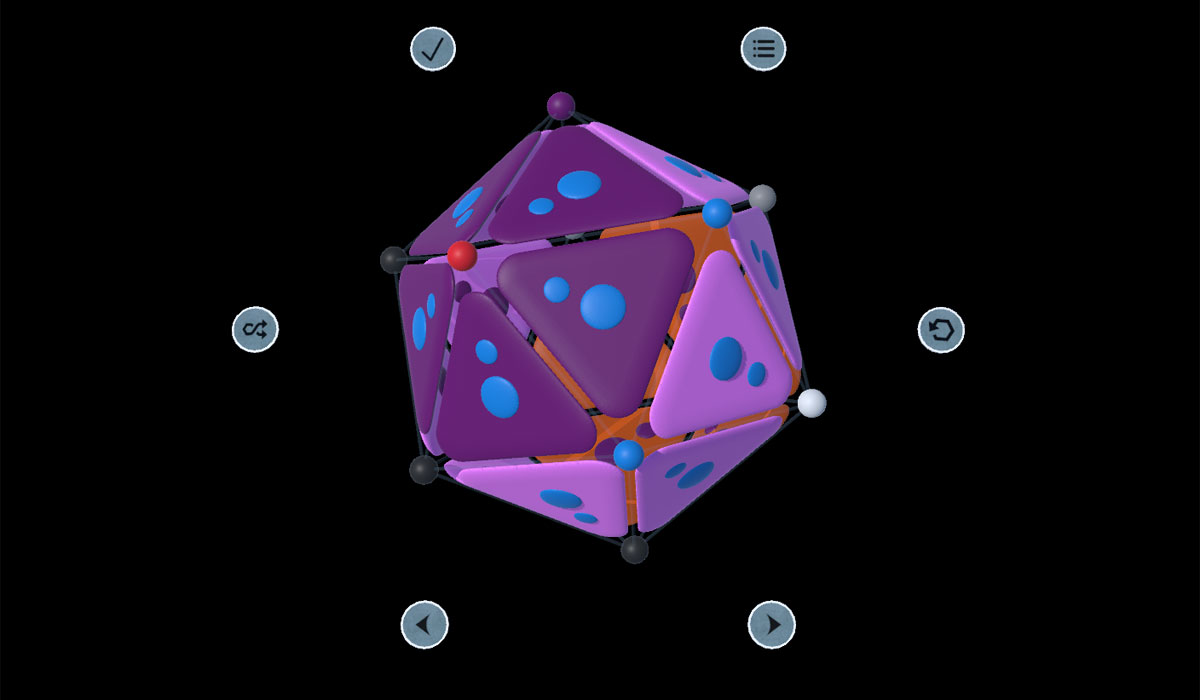
The Icosahedron :

RhombicDodecahedron :
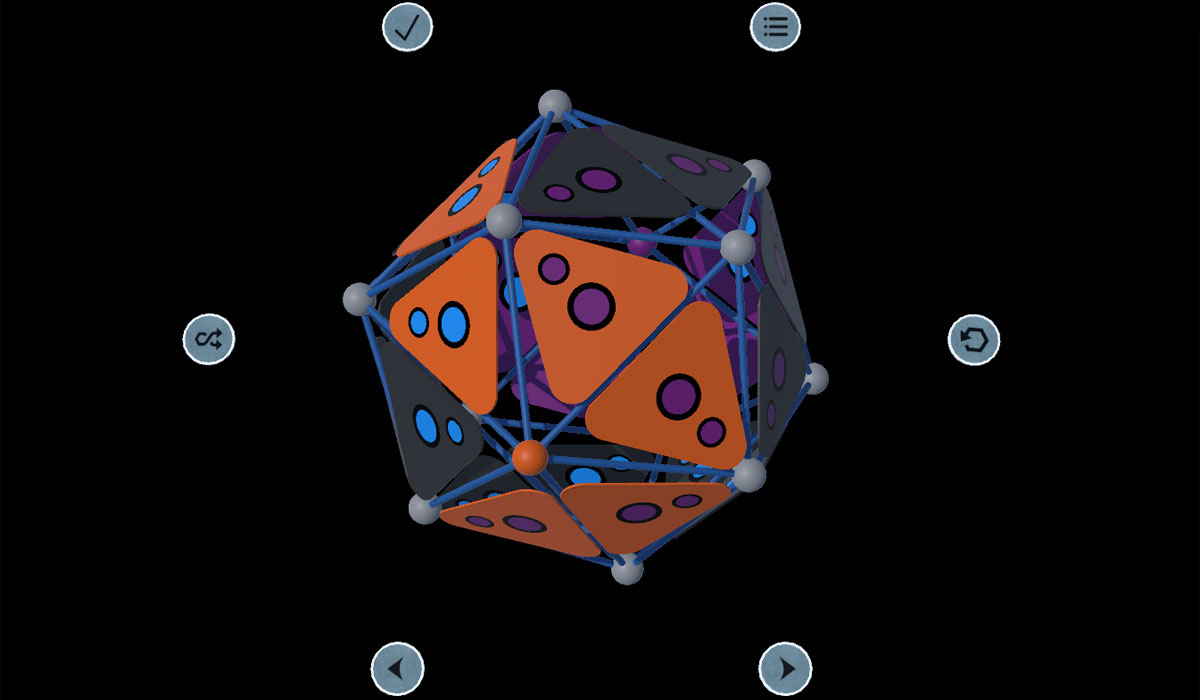
The Icosahedron is completely regular, while the Rhombic Dodecahedron short 'RoDo' (or its approximation here) is not. The Rodo therefore has gaps between the triangles and the symmetry lines, which does not interfere with gameplay. Playgrounds with bigger gaps between the edges and the triangles than 5° (i.e. bigger than in the 'Rodo') will not be used in the near future.
There are quite a lot of polyhedra that will be great to build the game on !
Tetrahedron (4 triangles) :

and the Octahedron (8 triangles) :

The small polyhedra (Tetra, Octa - hedra) have fewer triangles, and fewer patterns are possible.
The gamemode will therefore include randomized puzzles. Like the rubiks cube : you mix up the original and find your way back.
These small puzzles are actually rather difficult. Playing them almost feels like you're mixing it up more than solving it .. Just like making a mistake in the last few steps of solving the rubiks cube.
For example playing the tetrahedron, with every move you're changing 3 out of 4 existing triangles. You'll need to basically solve two positions parallel, and plan ahead on two closely linked tracks.
Apllied symmetry - rules and really thinking (what if ..) ahead is needed. Queueing doesn't work anymore.
Apllied symmetry - rules and really thinking (what if ..) ahead is needed. Queueing doesn't work anymore.
